为了促进数学与统计学院学科建设水平再上新台阶，交流偏微分方程的最新研究成果和发展动态，加强同相关领域专家的学术交流与合作，推动学院偏微分方程科研团队建设，黄淮学院决定于2022年6月29日-6月30日举办“非线性偏微分方程及应用”国际学术会议，会议邀请国内外偏微分方程领域著名专家学者参会并做报告，欢迎广大师生参加！

会议主题：非线性偏微分方程及应用

承办单位：数学与统计学院、黄淮学院科研处

会议地点：黄淮学院 9号楼502

腾讯会议号：896-6269-8848

联系人：卓然 18939692969；zhuoran1986@126.com

专家及报告题目

报告人：曹道民

报告人单位：中国科学院数学与系统科学研究院

报告人简介：

曹道民， 1983年6月毕业于湘潭大学数学专业，1989年6月在中国科学院获博士学位。现任中国科学院数学与系统科学研究院研究员、博士生导师。主要从事非线性偏微分方程和非线性分析的研究，独立或与人合作共发表论文130多篇，与人合作在Cambridge University Press出版专著一部。曾获国家杰出青年基金（2004年）和中国科学院青年科学家奖（1999年），曾任中国科学院数学与系统科学研究院应用数学研究所所长。曾主持过中国科学院知识创新工程重要方向性项目《数学物理中的若干重大问题》和中国科学院前沿重点项目《带间断非线性椭圆型方程》等科研项目。现任《应用数学学报》和《数学物理学报》副主编，是《Applicable Analysis》、《Annales Academiae Scientiarum Fennicae, Mathematica》等多种刊物的编委。

报告摘要：

三维不可压缩欧拉方程的涡丝一定是副法向曲率流，对任意一条按副法向曲率流演化的曲线是否有涡集中于该曲线附近的解是一个长期未决的公开问题，称之为涡丝猜想（vortex filament conjecture），该猜想仅在特殊情况得到解决。如该曲线是平面圆周，则对应于小截面涡环解的存在性。对小截面涡环解的存在性已有许多研究。报告人将报告和万捷（北京理工大学）最近关于3维不可压缩欧拉方程具有螺旋对称的小截面涡解的存在性的结果，这是涡丝猜想在曲线为螺旋对称的特殊情形。

报告人：陈文雄

报告人单位：Yeshiva大学

报告人简介：

陈文雄，Yeshiva大学数学系终身教授，南开大学特聘讲座教授（天津市千人）,曾多次获得美国国家科学基金奖，致力于偏微分方程、非线性泛函分析和几何分析等。研究方向主要包括：非线性偏微分方程正解的分类，几何不等式和黎曼流形上正解的性质等。论文发表在 Annals of Math, J. of Diff. Geom, Comm. Pure and Appl. Math, Duke Math. J, Advances in Math, Arch. Rat. Mech. Anal等著名国际数学期刊，他引已达五千余次。

报告摘要：

In this talk, I will summarize some of our recent results on the qualitative properties of positive solutions for nonlinear parabolic fractional equations

       (1)

including asymptotic radial symmetry of solutions, monotonicity of the entire solutions in half spaces, non-existence of entire solutions with indenite non-linearities, radial symmetry of ancient solutions in the whole space, and sliding method for fractional parabolic equations.

There have been a series of results for equation (1) if the fractional Laplacian is replaced by the regular Laplacian. However due to the non-locality of the fractional operator, many traditional approaches no longer work. We have introduced several new ideas and developed a series of new techniques to deal with the fractional cases. We believe that these new tools can be applied to solve many other nonlocal problems, both elliptic and parabolic.

I would like to mention that many ideas and results in dealing with fractional elliptic equations can be modified and then applied to study the fractional parabolic equations. I will use some simple examples to illustrate this.

报告人：陈志杰

报告人单位：清华大学

报告人简介：

陈志杰，2013年清华大学博士毕业，2013-2016年台湾大学博士后，2016年9月至今，清华大学数学系和数学中心副教授，博士生导师，研究领域是椭圆偏微分方程，迄今已发表论文40多篇，部分论文发表在Adv.Math、Amer.J.Math、Arch.Ration.Mech.Anal、Comm.Math.Phys、J.Differ.Geom、Math.Ann等著名期刊。

报告摘要：

In this talk, I will introduce our recent work joint with Dr. Houwang Li and Prof. Wenming Zou about the asymptotic behavior of positive solutions to the Lane-Emden system in planar domains.

报告人：桂长峰

报告人单位：University of Texas at San Antonion

报告人简介：

桂长峰教授于1991年获得美国明尼苏达大学博士学位。目前是德克萨斯大学圣安东尼奥分校(University of Texas at San Antonion)的Dan Parman Endowed Professor。1984年在北京大学获学士学位，1987年在北京大学获硕士学位，1991年在美国明尼苏达大学获得博士学位。曾任纽约大学库郎研究所讲师，加拿大哥伦比亚大学助理教授、副教授，美国康尼迪格大学副教授、教授。2013年评选为美国数学会会士，曾获得加拿大太平洋数学研究所研究成果奖，加拿大数学中心Aisensdadt奖，IEEE最佳论文奖，中国国家自然科学基金海外合作基金。他主要从事偏微分方程理论研究，特别在Allen-Cahn方程的研究，Moser-Trudinger不等式最佳常数的猜想等方面取得了一系列在国际上有重大影响的工作，在国际一流数学学术期刊发表论文50余篇，其中包括Annals of Mathematics, Inventiones Mathematicae等顶级期刊。

报告摘要：

In this talk, I will present recent results on Liouville-type theorems for the steady incompressible Navier-Stokes system in a three-dimensional slab with either no-slip boundary conditions or periodic boundary conditions. When the no-slip boundary conditions are prescribed, we prove that any bounded solution is trivial if it is axisymmetric oris bounded, and that general three-dimensional solutions must be Poiseuille flows when the velocity is not big. When the periodic boundary conditions are imposed on the slab boundaries, we prove that the bounded solutions must be constant vectors if either the swirl velocity is independent of the angular variable, or decays to zero as r tends to infinity, The proofs are based on the fundamental structure of the equations and energy estimates. The key technique is to establish a Saint-Venant type estimate that characterizes the growth of Dirichlet integral of nontrivial solutions. The talk is based on a recent joint work with Jeaheang Bang, Yun Wang and Chunjing Xie.

报告人：何其涵

报告人单位：广西大学

报告人简介：

何其涵，博士，硕士生导师，现任职于广西大学数学与信息科学学院。主要研究方向是偏微分方程，现主持国家自然科学基金地区基金1项，曾主持国家自然科学基金青年基金1项，国家自然科学基金天元基金1项，广西自然科学基金青年基金1项等，参与多项省部级及以上项目。在JMAA, ADE等杂志上发表论文十多篇。

报告摘要：

We consider the existence and nonexistence of positive solution for the following Brézis-Nirenberg problem with logarithmic perturbation:

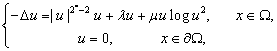
where  is a bounded smooth domain,   and is the critical Sobolev exponent for the embedding  The uncertainty of the sign of  in  has some interest in itself. We will show the existence of positive ground state solution which is of mountain pass type provided  and  While the case of  is thornier. However, for   we can also establish the existence of positive solution under some further suitable assumptions. And a nonexistence result is also obtained for  and  if Comparing with the results in Brézis, H. and Nirenberg, L. (Comm.PureAppl.Math. 1983), some new interesting phenomenon occurs when the parameter  on logarithmic perturbation is not zero.

报告人：黄耿耿

报告人单位：复旦大学

报告人简介：

黄耿耿，复旦大学数学科学学院副教授，博士生导师。师从洪家兴院士，后在上海交通大学做博士后研究，期间到台湾大学访问林长寿教授，入选2019年度上海市青年科技启明星计划，主要从事偏微分方程的理论研究。在Comm. Pure Appl. Math.,Comm. Partial Differential Equations，SIAM J. Numer. Anal.，Calc. Var. Partial Differential Equations, J. Differential Equations等国际著名数学期刊期刊上发表论文20余篇。黄耿耿副教授获得国家基金2项，现主持在研国家基金面上项目1项。

报告摘要：

In this talk, we talk about the uniqueness of the nontrivial solutions of some degenerate Monge-Ampere equations.

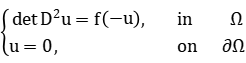
Under suitable conditions on f(t), we can show u is symmetric as  is symmetric. Then we can show the nontrivial solution u is unique by showing the non-degeneracy of the linearized equation for some special f(t). This is a joint work with Cheng Tingzhi.

报告人：刘祥清

报告人单位：云南师范大学

报告人简介：

刘祥清，云南师范大学教授，主要研究领域：非线性泛函分析，主要是利用临界点理论研究非线性椭圆边值问题。2009年获得苏州大学博士学位，2010年8月破格晋升为副教授，2011年8月破格晋升为教授。2017年10月-2018年10月在德克萨斯大学泛美分校学术访问。主持完成国家自然科学基金3项、省部级项目2项。2011年获得云南省第十届科技论文奖“一等奖”，2015年10月入选云南省中青年学术技术带头人后备人才，2019年获得云南省自然科学奖“一等奖”。主要研究成果发表于CVPDE, JDE, Pro.Amer.Math.Soc.等国际学术期刊。

报告摘要：

We consider quasilinear elliptic equations, including the following Modifified Nonlinear Schrodinger Equation as a special example:

\begin{equation*}

\begin{cases}

\Delta

u+\frac{1}{2}u\Delta u^2+\lambda|u|^{r-2}u=0,~~~\text{in}~\Omega,\\

u=0~~~\text{on}~\partial\Omega.

\end{cases}

\end{equation*}

where Ω ⊂ R^N (N ≥ 3) is a bounded domain with smooth boundary, λ > 0, r ∈ (2, 4). We prove as λ becomes large the existence of more and more sign-changing solutions of both positive and negative energies.

报告人：孙玉华

报告人单位：南开大学

报告人简介：

孙玉华，南开大学数学学院副教授，博士生导师，研究方向为黎曼流形及图上的分析，包括椭圆及抛物方程，在包括CPAM，JFA, Math. Annalen, CVPDE等著名期刊发表学术论文近20篇。

报告摘要：

We investigate the non-existence and existence of positive solutions to biharmonic elliptic inequalities  on manifolds. Using Green function and volume growth conditions, we establish the critical exponent for biharmonic problem. This is based on joint work with Yadong Zheng.

报告人：陶有山

报告人单位：上海交通大学

报告人简介：

陶有山，上海交通大学数学科学学院特聘教授。曾先后于南京大学、复旦大学、苏州大学获得数学学士、硕士和博士学位。主要研究方向为偏微分方程，特别是趋化交叉扩散方程，已在数学期刊（其中包括：JEMS, PLMS, JFA, SIAP, SIMA, Ann. I. H. Poincare）上发表论文90余篇，MR引用3400余次；2018-2021年连续四年入选科睿唯安“全球高被引科学家”。现担任数学期刊Nonlinear Analysis: RWA和EMS Surveys in Mathematical Sciences (EMSS) 的编委。

报告摘要：

This talk reports a recent co-work, with Michael Winkler (Paderborn)，on a pursuit-evasion system that describes a fully cross-diffusive interaction mechanism between predators and preys. The system formally possesses two basic entropy-like structures, but the regularity thereby implied seems insufficient to ensure global solvability for large data. We design a suitable thin-film-type approximation which allows us to develop a theory not only of global weak solvability, but also of qualitative behavior.

报告人：王术

报告人单位：北京工业大学

报告人简介：

王术，教授，博士生导师。现为北京工业大学教授，北京工业大学数学一级学科博士学位授权点责任教授。曾任中国数学会理事、中国工业与应用数学会理事，北京工业大学应用数理学院院长等职务。2016年获得国务院政府特殊津贴。1990年河南大学本科毕业，1993年北京理工大学硕士研究生毕业，1998年南京大学博士研究生毕业。曾在中科院数学所和奥地利维也纳大学做博士后，曾在美国加州理工学院做高级访问学者。主要研究：偏微分方程及其应用。现主持或曾主持国家自然科学基金8项（含重点项目1项），独立获得北京市科学技术奖二等奖1项，出版著作3部，在《Adv. In Math.》《ARMA》《SIAM J Math Anal》《CPDE》《J. Diff. Eqns》等杂志发表SCI收录学术论文100余篇。

报告摘要：

The global well-posedness the initial-boundary value problem on incompressible Navier-Stokes equations and the related models in the domain with the boundary is studied. The global existence of a class of weak solution to the initial boundary value problem to two/three-dimensional incompressible Navier-Stokes equation with the pressure-velocity relation at the boundary is obtained, and the global existence and uniqueness of the smooth solution to the corresponding problem in two-dimensional case is also established. Some extends to the corresponding incompressible fluid models such as Boussinesq equation and FSI models etc. are given.

报告人：叶东

报告人单位：华东师范大学

报告人简介：

叶东，现任华东师范大学数学科学学院教授。1990年毕业于武汉大学中法数学班，1994年在法国卡尚高等师范学院获得博士学位，后长期在法国大学任职，回国前是法国洛林大学的一级教授。主要研究领域是非线性偏微分方程和几何分析。入选第国家级人才项目，于2018年9月全职回到华东师范大学工作。

报告摘要：

Hardy-Rellich type inequalities have broad applications in different fields of analysis and geometry, they have been studied extensively since Hardy's seminal works one century ago. In this talk, we will revise various first order Hardy inequalities, and point out that most of them can be obtained by a simple and unified equality. This approach permits us to get some new or improved first order Hardy inequalities. We will explain also our approach to obtain higher order Hardy-Rellich type equalities which imply and improve many classical Hardy-Rellich inequalities. This is a joint work with Xia Huang at ECNU.

报告人：张志涛

报告人单位：中国科学院数学学院系统科学研究院 & 江苏大学

报告人简介：

张志涛，教授，博士生导师，博士，江苏大学数学科学学院院长，中国科学院数学与系统科学研究院二级研究员、博士生导师, 中国科学院特聘研究员（核心骨干），中国科学院大学岗位教授。国家杰出青年基金获得者、领军人才、科技部中青年科技创新领军人才、洪堡学者。Springer期刊Partial Differential Equations and Applications主编。主要研究方向：非线性泛函分析和偏微分方程。

报告摘要：

我们利用拓扑方法、分歧理论和移动平面法研究完全非线性椭圆方程（组），特别研究Monge-Ampère equations and k-Hessian equations在不同区域上解的存在唯一性、解的个数估计、解的对称性，给出一些新结果。